Example 6a: Bayesian Network 'Student Model' with Evidence
Example 6a: Bayesian Network 'Student Model' with Evidence
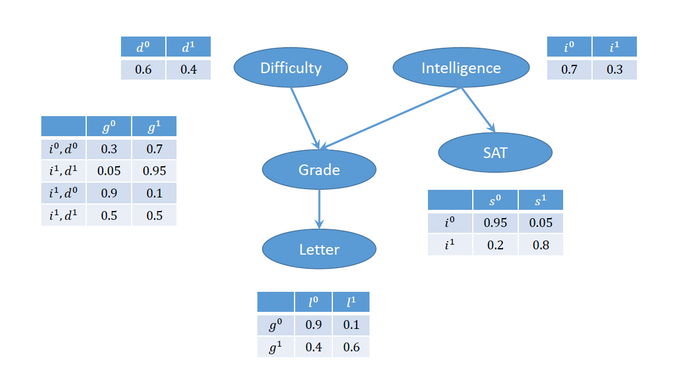
DAG of Bayesian Network 'Student Model'
Andrew D. Gordon, Thomas A. Henzinger, Aditya V. Nori, and Sriram K. Rajamani. 2014. Probabilistic programming. In Proceedings of the on Future of Software Engineering (FOSE 2014). ACM, New York, NY, USA, 167-181. DOI=10.1145/2593882.2593900 doi.acm.org/10.1145/2593882.2593900
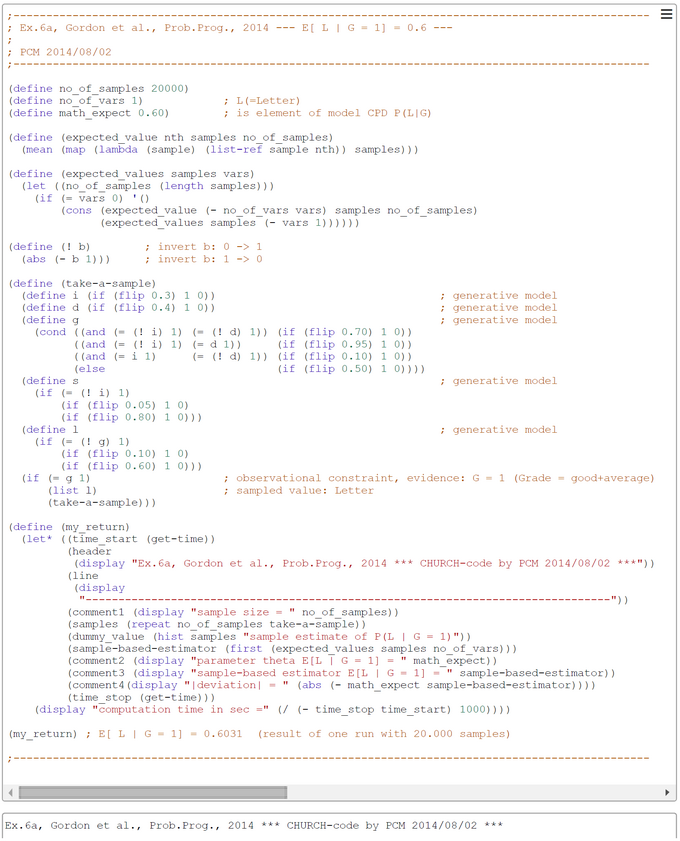
Example 6a: PROB-Code for Bayesian Network 'Student Model' with evidence

"Bayesian Networks can be used to pose and answer conditional queries, and this can be encoded in probabilistic programs using observe statements. For example, we can ask the question P(L | G = g1) which asks for the probability distribution (or the expected value of L, given that we observe G = g1). Such a question can be encoded as a probabilistic program shown left. At line 12 the observe statement observe(g = 1) conditions the value of g to 1. Then, at line 21 the program returns l. Thus, the meaning of the program is equal to P(L | G = g1).
In general, every Bayesian Network can be encoded as an acyclic probabilistic program in a straightforward manner, and conditioning can be modeled using observe statements in the probabilistic program." (Gordon et al., 2014)
Here is a summary of the domains due to the modifications of Gordon et al. (2014):
Val(D) = <d0, d1> = <easy, hard>
Val(I) = <i0, i1> = <non smart, smart>
Val(G) = <g0, g1> = <A, B+C>
= <excellent, good+average>
Val(S) = <s0, s1> = <low score, high score>
Val(L) = <l0, l1>
= <strong_letter, weak_letter>
Ex6a: CHURCH-Code for Bayesian Network 'Student Model' with inference P(L | G=1)
The PROB-code snippet from Gordon et al. is translated by us to a functional CHURCH-program to clarify its semantics. The generative model is contained in the CHURCH function "take-a-sample". What is a bit puzzling is that in example 6a the authors chose with the conditional probability P(L | G=1) a direction of inference which is the same as in the generative Bayesian network. So the to be inferred conditional probability P(L | G=1) = P(Letter | Grade=good+average) could be obtained by a simple look up in the local CPD P(L | G). Despite of this we implemented the CHURCH program with the same inference direction to demonstrate the usefulness of the simple rejection sampling scheme.
Here is a summary of the domains due to the modifications of Gordon et al. (2014):
Val(D) = <d0, d1> = <easy, hard>
Val(I) = <i0, i1> = <non smart, smart>
Val(G) = <g0, g1> = <A, B+C> = <excellent, good+average>
Val(S) = <s0, s1> = <low score, high score>
Val(L) = <l0, l1> = <strong_letter, weak_letter>
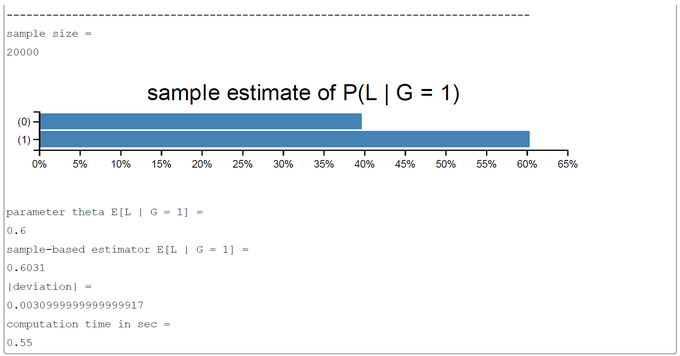
The number of samples taken was set to 20000 in this run. This number could in principle be increased to get a better precision of estimates. The sampling method used is the simple-to-understand 'forward sampling'. The screen-shot presented was generated by using the PlaySpace environment of WebCHURCH.
The inferred E(L | G=1) = P(L=1 | G=1) is near 0.60, so the verbal interpretation is "If you have a good or average grade, the probability of a weak recommendation letter is approximately 0.60".