Lesson3: Particle Filter - Generation of Particles-
Lesson3: Particle Filter - Generation of Particles-
Generation of N Random Particles (= Random Positions in the RobotWorld)

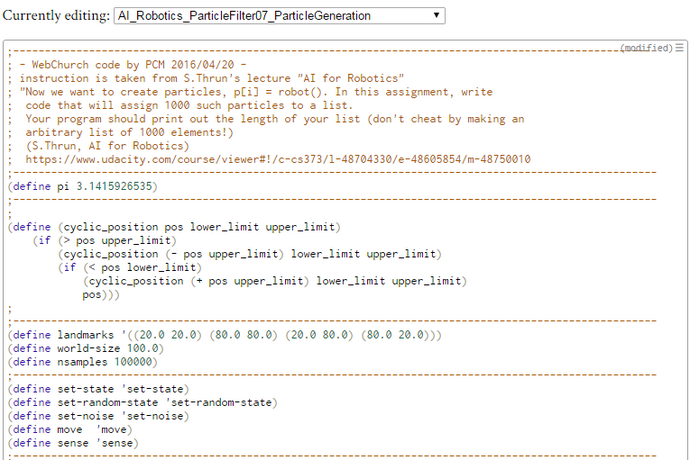

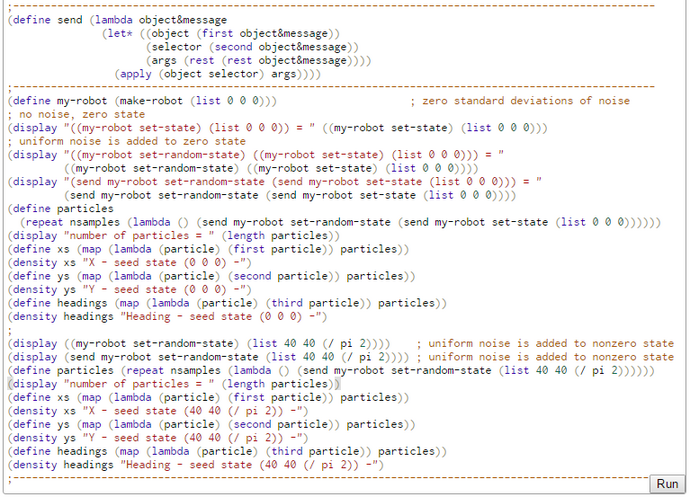
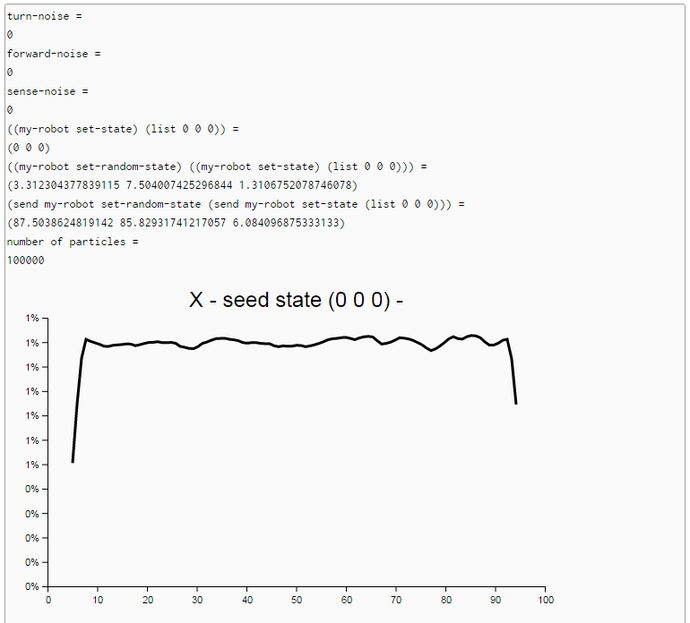
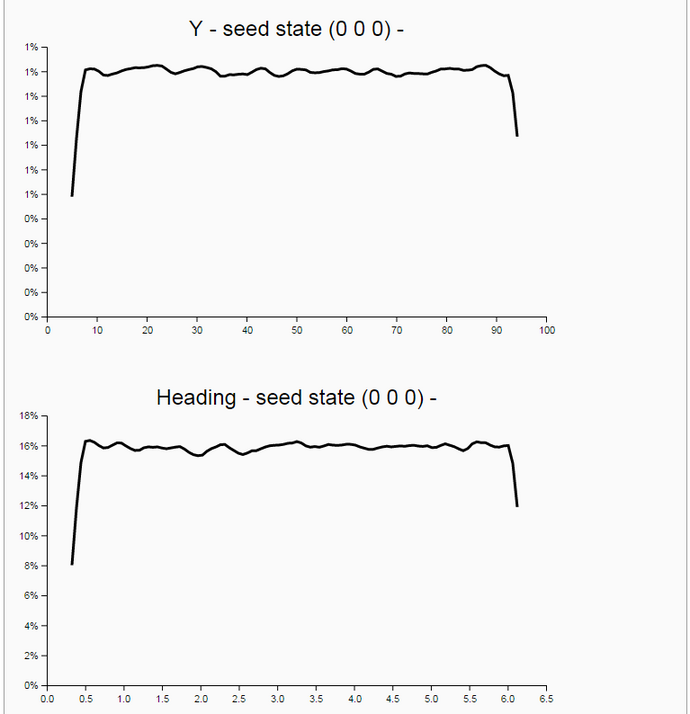
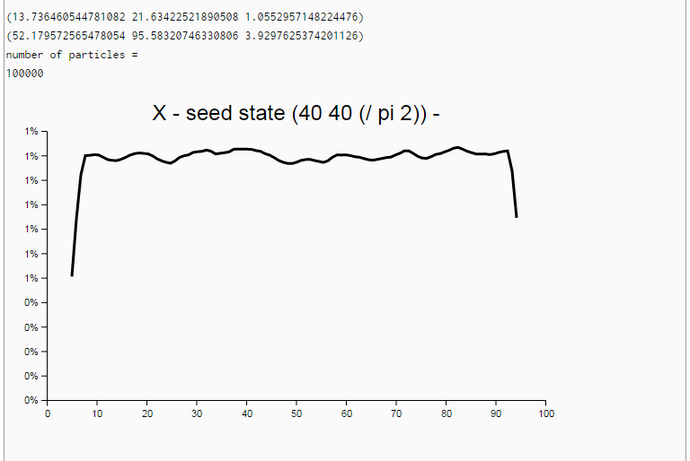
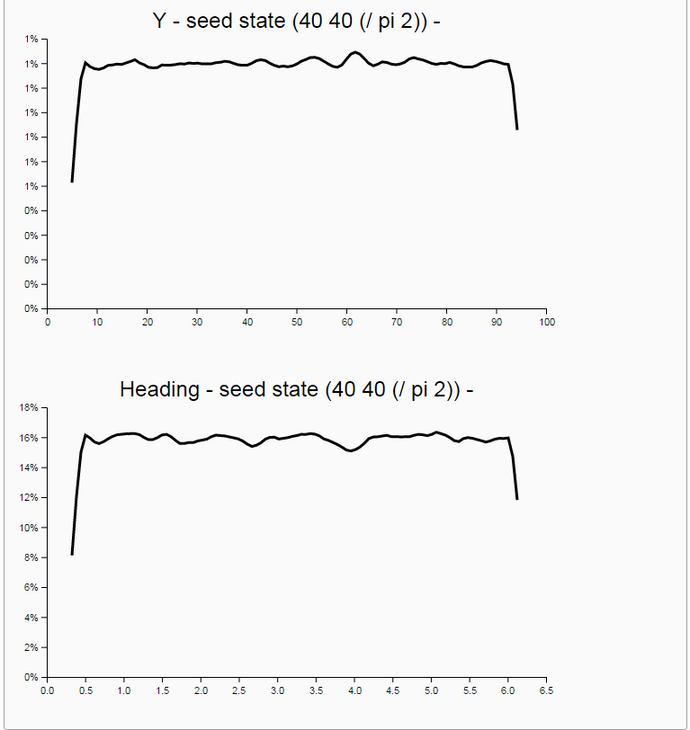
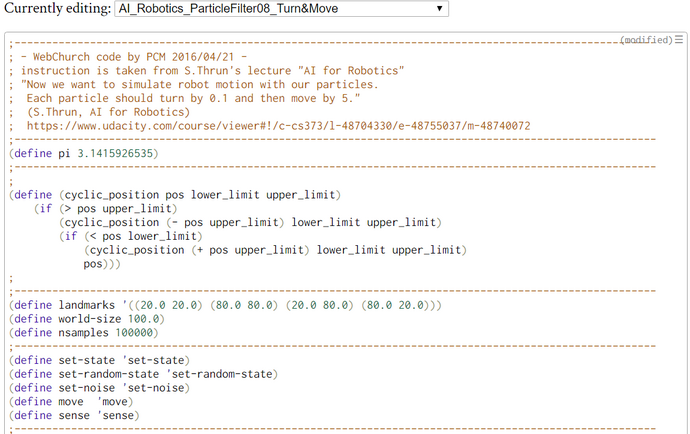
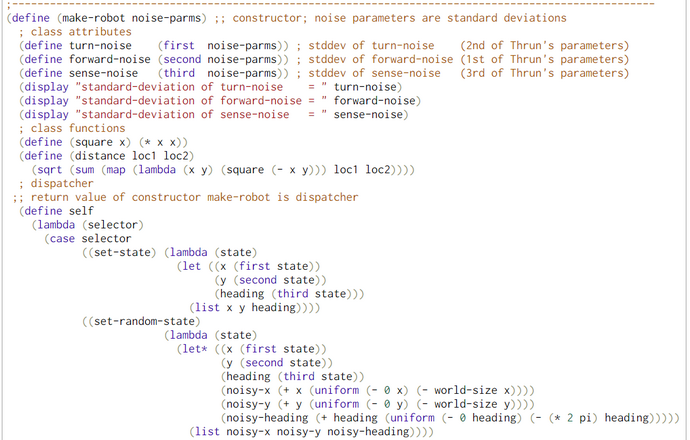
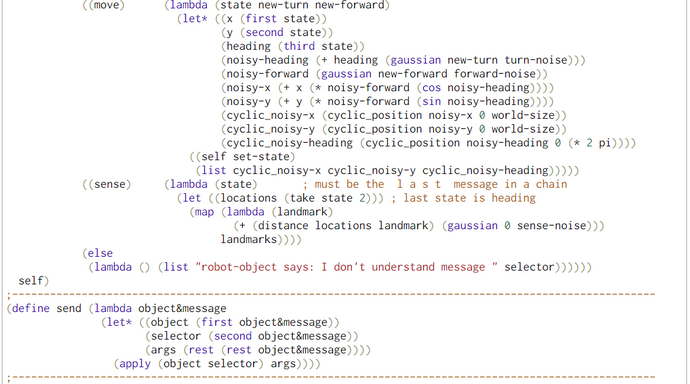
Generation of N Random Particles with Turn and Forward Motion (WebChurch)
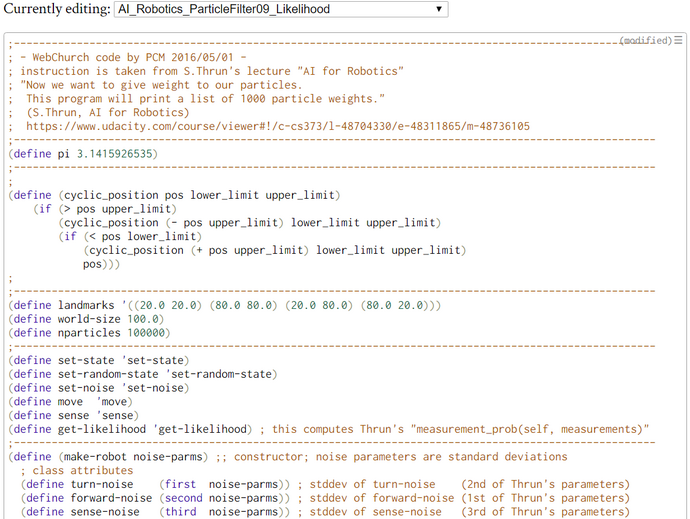
The Likelihood of the Particles (WebChurch)
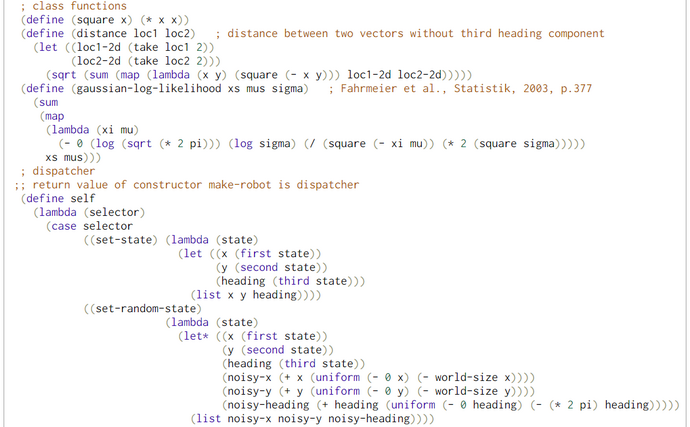
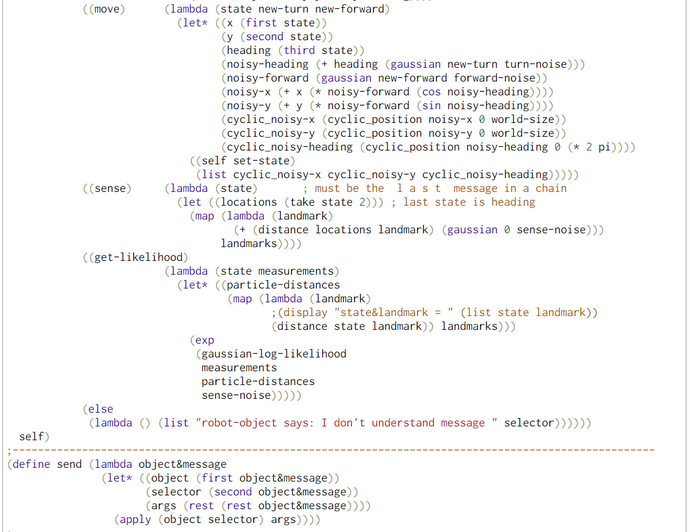
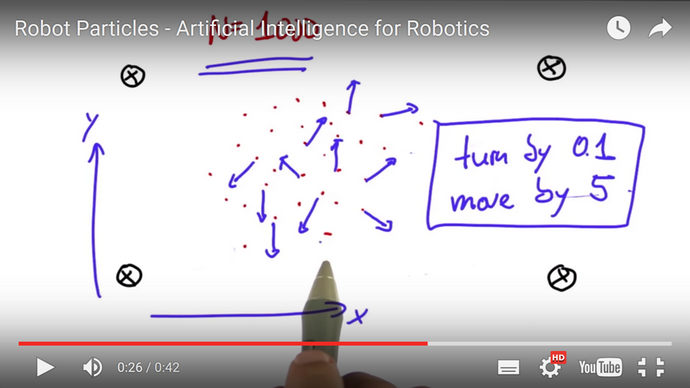
From the viewpoint of the agent "my-robot" a map with landmarks is necessary for determining his own global position: this position in reality and on the map is unknown. The only information the bot knows with some uncertainty are the distances (= evidence, measurements) to the landmarks. From a Bayesian pointof view the position on the map is the latent state and the distance set is the evidence. What we want to get by inference is the posterior P(States | distance-evidence).
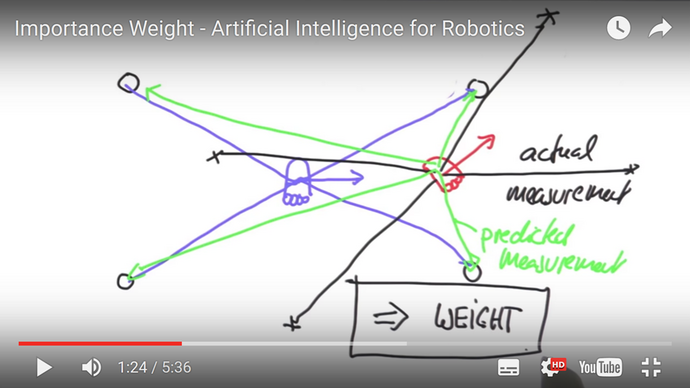
The bot asks the Particle Filter Oracle. This oracle generates N randomized trial positions (called "particles"). In contrast to the position of the bot the positions of all particles are known. So the distances from each particle's position to the landmarks can be measured. Now, the real measurements of the agent my-robot are compared to the virtual measurements of the particle in the virtual world (the map). The greater the similarity of the two sets of measurements are the greater is the likelihood that the particle has a position in the map which is similar (near) to the position of the agent my-robot in the real world.
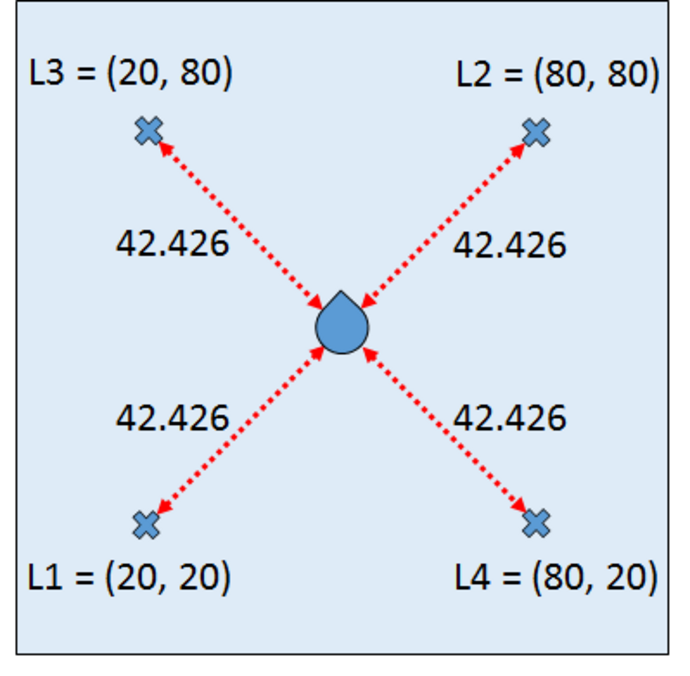
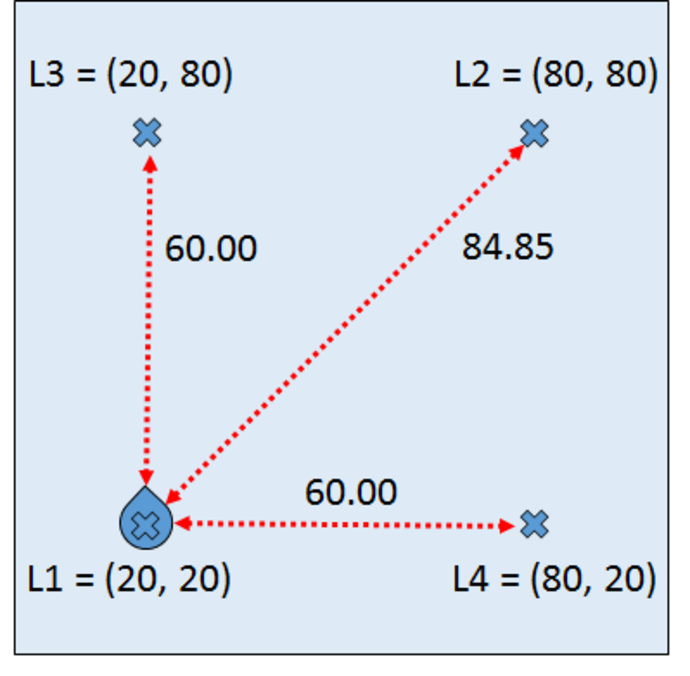
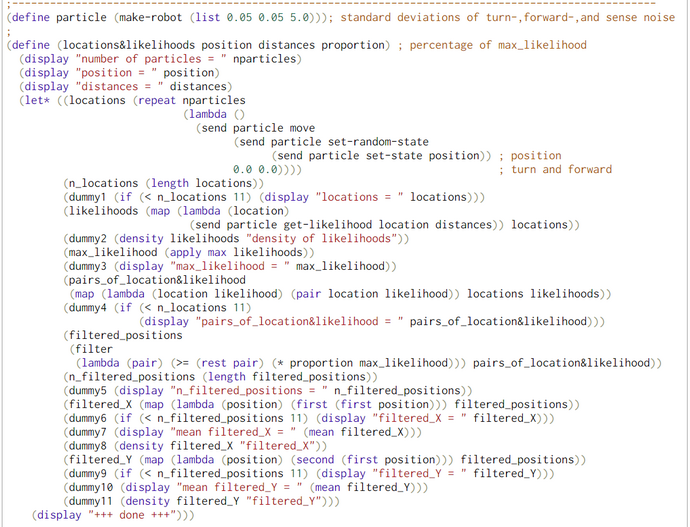
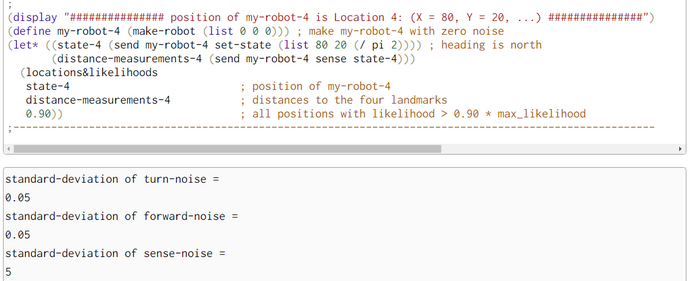
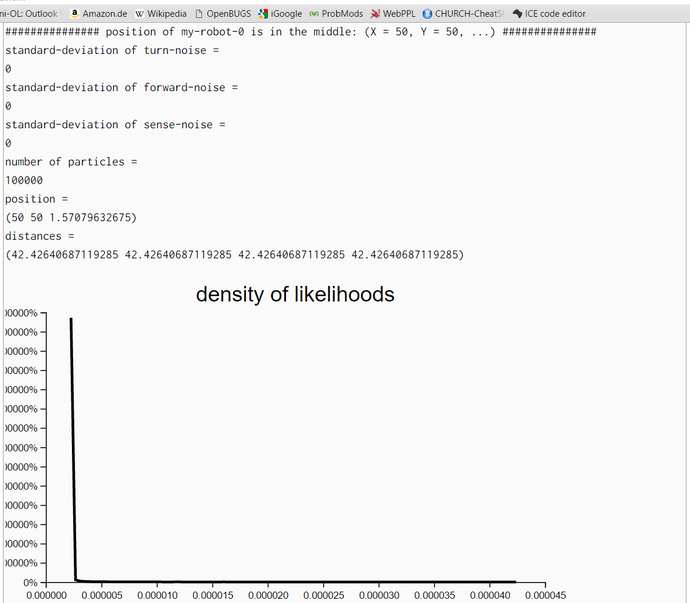
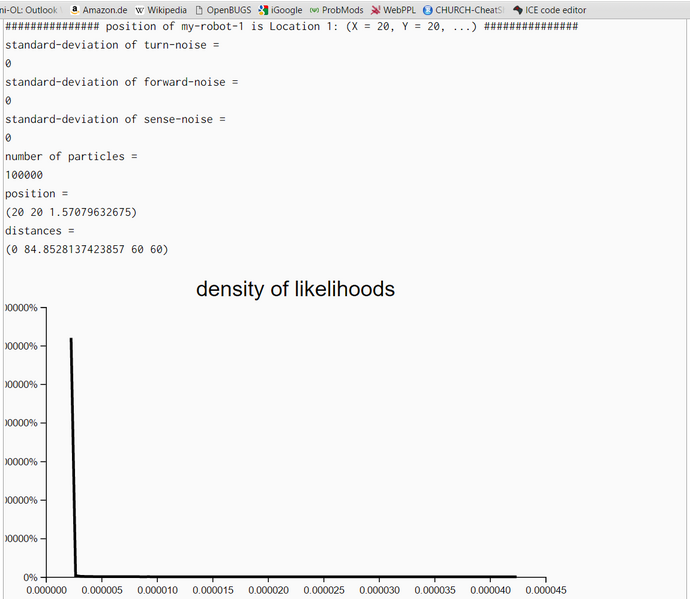
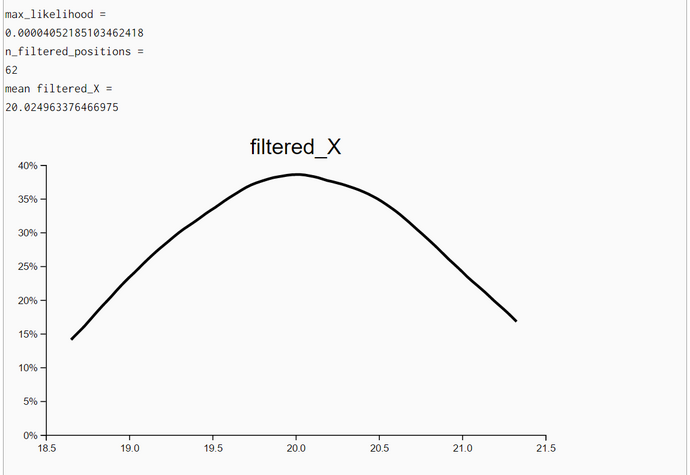
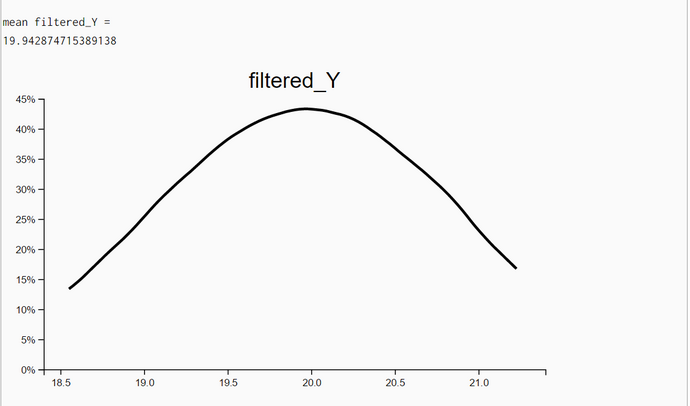
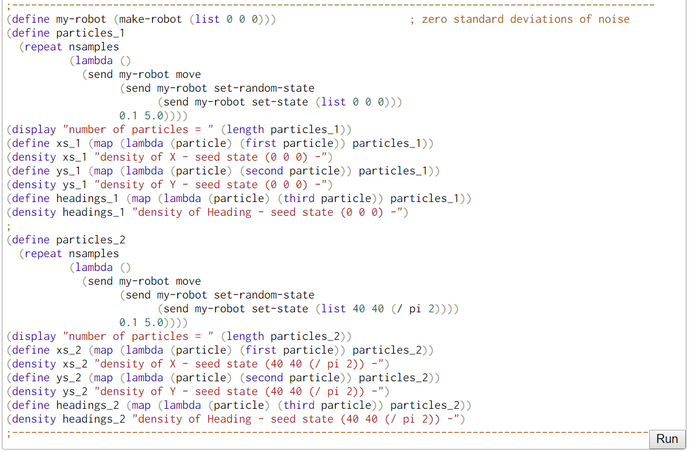
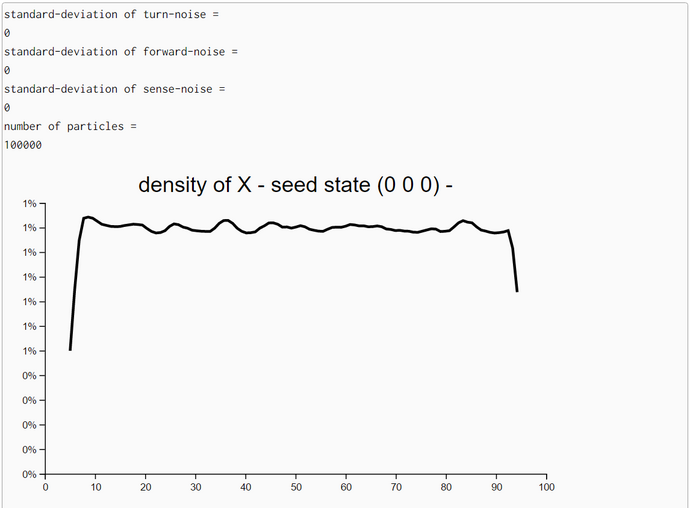
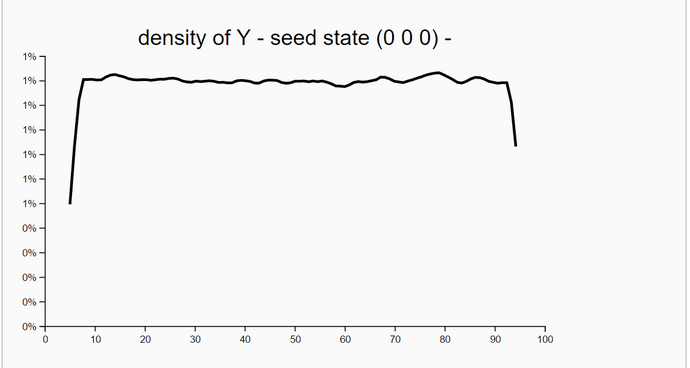
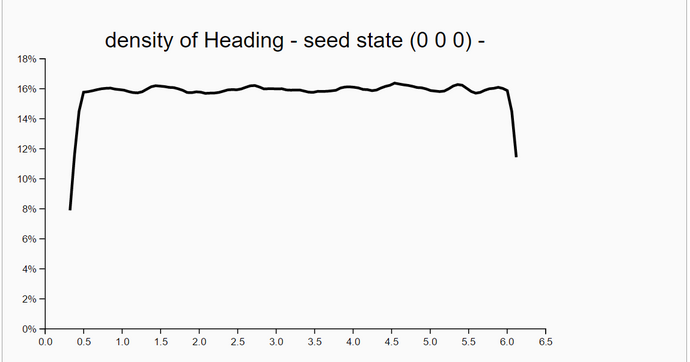
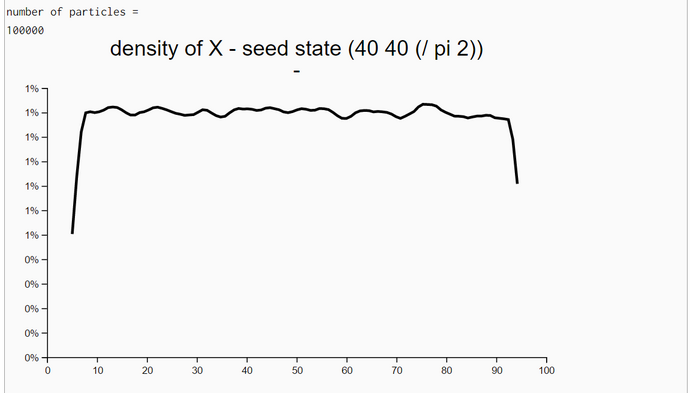
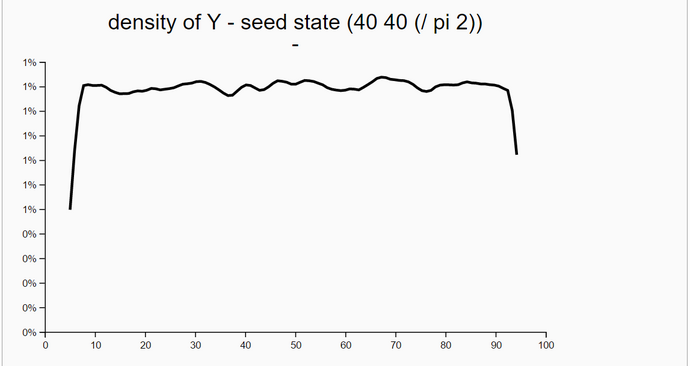
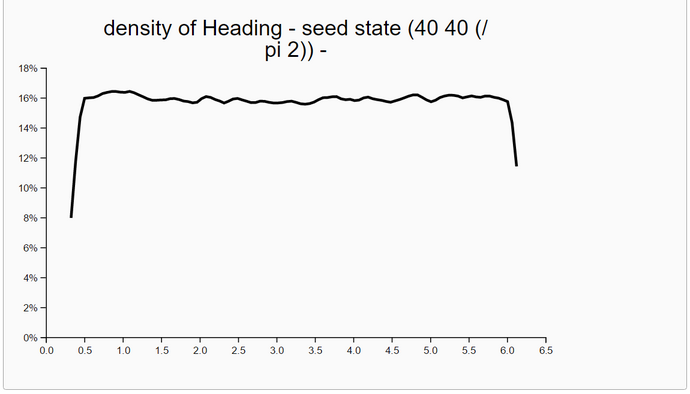
To check the correctness of our WebChurch code we ran five simulation runs with different seed positions. The first was in the middle of our world. The coordinates are (X = 50, Y = 50). This seed position is unknown to the robot. His distance measurements to the four landmarks are sqrt(30^2+30^2) = sqrt(1800) = 42.426. The other four seed positions are identical to the four landmarks. So for landmark 1 the seed position is (X = 20, Y = 20) and the distance evidence to landmarks 1-4 are '(0.0 84.85 60.0 60.0).
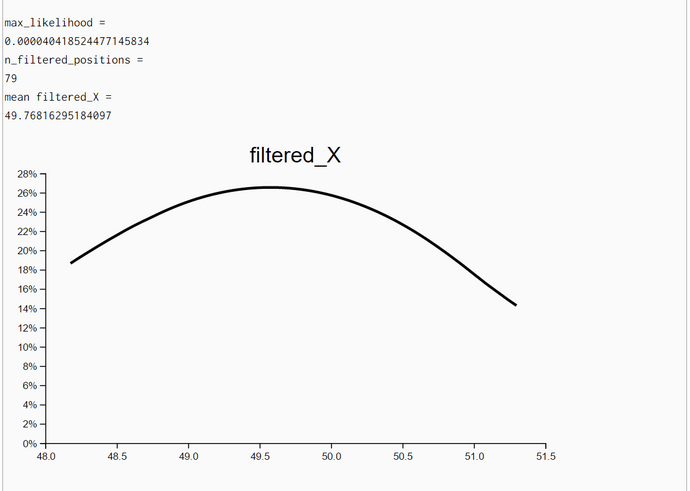
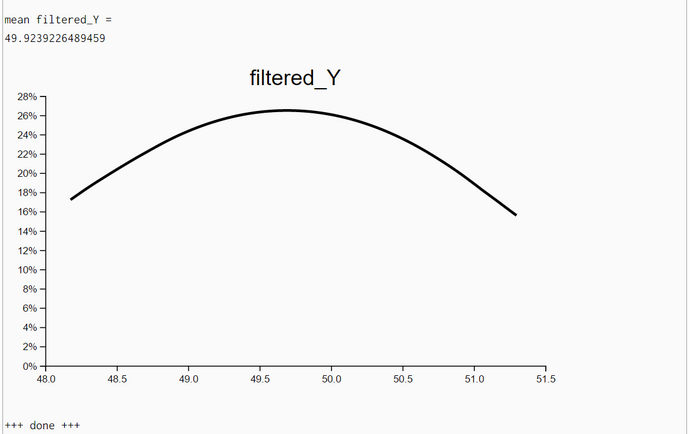
We generated in each run N = 100000 particles and computed their likelihoods. Then, we filtered all particles so that we retained all particles with likelihoods greater than 90% of the maximum likelihood. Then we estimated the density of these high-likelihood particles. As expected the coordinates of the highest-likelihood particles are very near the seed points.