High-order perturbation theory for strongly correlated Boson systems
High-order perturbation theory for strongly correlated Boson systems
Quantum phase transitions
Quantum phase transitions are driven by quantum fluctuations instead of thermal fluctuations, and therefore occur even at temperature T=0. An archetypal system exhibiting this phenomenon is given by the Bose-Hubbard model, which describes interacting Bose particles on a lattice: The particles may tunnel between neighbouring lattice sites which are connected by an hopping matrix element J, while particles sitting on the same site repel each other with an energy U per pair. Whereas the kinetic energy is minimized with increasing delocalization of the particles, the repulsion energy is minimized when the particles are localized at individual sites; the competition between these two opposing tendencies gives rise to a quantum phase transition from a Mott insulator to a superfluid upon increase of the scaled tunneling strength J/U.
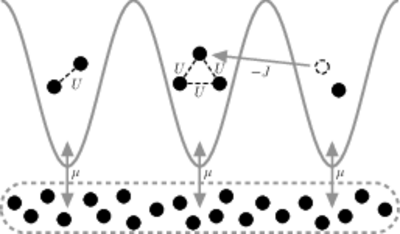
The accurate calculation of the model's phase diagram in the parameter plane spanned by the system's scaled chemical potential mu/U and the scaled tunneling strength J/U has long constituted a benchmark problem for computational many-body physics. Our approach to this problem rests on a combination of numerically executed, high-order diagrammatic perturbation theory, and analytic continuation of the diverging perturbation series with the help of generalized hypergeometric functions. In this manner, we are determining the divergence exponents ε2k which characterize the k-particle correlation functions at the transition.
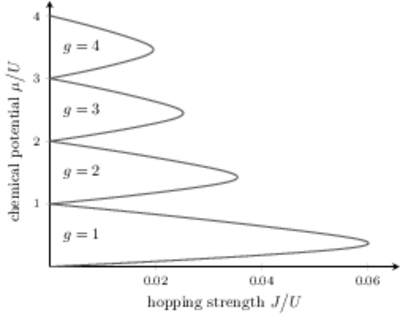
At the tip of the Mott lobes, the d-dimensional Bose-Hubbard model falls into the universality class of the (d+1)-dimensional XY model, so that the critical exponents provided by the two-dimensional Bose Hubbard model should equal those of the precisely measured lambda transition undergone by liquid helium. We have established the connection
βc = ε2/4
between the critical exponent βc of the order parameter and the divergence exponent ε2, and have utilized this relation for providing novel evidence for the validity of the universality hypothesis.
For details, see Sören Sanders and Martin Holthaus,
New J. Phys 19, 103036 (2017), and J. Phys. A: Math. Theor. 50, 465302 (2017).


